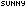【竞赛】设x、y都是正整数,且使根号(x-116)+根号(x+100)=y,则y 的最大值是多少?
作者:随然 日期:2009-11-14
题目:设x、y都是正整数,且使根号(x-116)+根号(x+100)=y,则y 的最大值是多少?
解答:
设 x-116=a^2 , x+100=b^2 (b>a)
则 b^2-a^2=(x+100)-(x-116)=216
所以 (b-a)(b+a)=216
所以 b-a取最小值时b+a为最大值
因为x,y为正整数,所以b^2,a^2为正整数,a,b为正整数
当b-a=1时,无整数解
当b-a=2时,a=53,b=55,满足题意
所以y的最大值为b+a=108
若该题求的是y的最小值,那么就可以分解216=2*2*2*3*3*3,(b-a)(b+a)=2*2*2*3*3*3
所以b+a的值可能为2,4,6,8,9,12,18,24,27,36,54,72,108
从2开始取,只要能解出a,b为正整数,则就满足题意。
[本日志由 随然 于 2009-11-14 11:32 PM 编辑]
 上一篇: 取消开始菜单中的“文档”和不记录最近打开的文档
上一篇: 取消开始菜单中的“文档”和不记录最近打开的文档 下一篇: 论坛发贴数级别方案
下一篇: 论坛发贴数级别方案 文章来自: 本站原创
文章来自: 本站原创 Tags: 数学
Tags: 数学  相关日志:
相关日志:
评论: 0 | 引用: 0 | 查看次数: 31533
发表评论