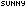三角形ABC,E、F三等分AC,BC边上DB=2DC,连接BE,BF,AD相交于H,G,求四边形EF

题目：三角形ABC,E、F三等分AC,BC边上DB=2DC,连接BE,BF,AD相交于H,G,求四边形EFGH的面积为ABC面积的几分之几？

解：设△ABC的面积=m.连结CG，设△CDG的面积=s，△CFG的面积=t,则△BDG的面积=2s，△AFG的面积=2t，于是有
3s+t=(1/3)m,
s+3t=(1/3)m.
两式相加，得4s+4t=(2/3)m,即s+t=(1/6)m.
也就是四边形CDGF的面积=(1/6)m.
连结CH，设△CDH的面积=x,△CEH的面积=y，则△BDH的面积=2x，△AEH的面积=(1/2)y.于是有
3x+y=(2/3)m…………①
x+(3/2)y=(1/3)m……②
解由组成的方程组，得
x=(4/21)m,y=(2/21)m.
∴x+y=(4/21)m+(2/21)m=(2/7)m,即四边形CDHE的面积=(2/7)m.
∴ 四边形EFGH的面积=四边形CDHE的面积-四边形CDGF的面积=(2/7)m-(1/6)m
=(5/42)m.
即四边形EFGH的面积是△ABC的面积的5/42

解法二：
先用平行线分线段成比例，得出
BH＝6*EH BG＝3*GF
所以　三角形BGH的面积＝(3*6)/(4*7) 倍的三角形BEF的面积
即　三角形BGH的面积＝9/14 * 三角形BEF的面积
所以　四边形EFGH＝5/14 * 三角形BEF的面积
因为　三角形BEF的面积＝1/3 * 三角形ABC的面积
所以　四边形EFGH＝5/14 * 1/3 * 三角形ABC的面积＝5/42 * 三角形ABC的面积

四边形EFGH的面积为ABC面积的5/42

上一篇: 已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点
下一篇: ASP版HTML新闻内容自动分页程序
文章来自: 本站原创
引用通告: 查看所有引用 | 我要引用此文章
Tags: 数学
相关日志: